浅谈拓扑优化方法

拓扑优化（topology optimization）是根据给定的载荷工况、约束条件和性能指标等，在给定的区域内对材料分布进行优化的数学方法，是结构优化的一种形式。通过拓扑优化可以得到最优的传力路径以及满足规定的减少材料量的同时最大化结构刚度的结构形式。

实际上现在结构优化可以主要分为三类：尺寸优化、形状优化、拓扑优化。这三类也分别对应着产品设计的几个阶段：拓扑优化——概念设计阶段；形状优化——基本设计阶段；尺寸优化——详细设计阶段；而这几种优化的形式现在市场上几乎以尺寸优化以及形状优化为主，而拓扑优化却广泛应用于航空航天、机械、建筑等领域，而对于国内的传统制造业而言拓扑优化仍旧有较大的发展空间，相信拓扑优化结合增材制造工艺以及3D打印技术会对未来的结构设计有很大的变革。当然我们身边也有很多关于拓扑优化的例子如下图所示：

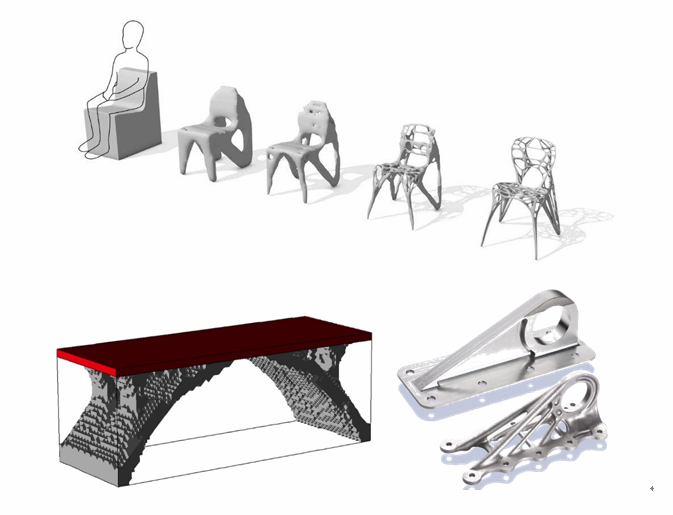
关于拓扑优化的方法可分为离散体结构（Discrete structure）和连续体结构（Continuum structure）拓扑优化方法，以桁架为代表的离散体结构拓扑优化方法旨在满足一定边界条件下，确定各杆件的最佳尺寸以及最佳的连接方式，该与拓扑优化方法设计变量少且计算效率高；与离散体结构拓扑优化相比较，连续体结构拓扑优化需要建立相对较好的有限元模型，计算效率低，但是对于拓扑对象不是桁架结构类时，采用连续体结构就相对更加精准一些。

对于连续体结构拓扑优化一般是指在给定的载荷以及约束条件下，确定连续体内有无孔洞以及孔洞的位置、数量和形状等，进而确定性能最佳的材料分布。从理论上讲，连续体设计域中的坐标点是无穷的，因此需要利用有限元的方法将连续问题离散化，再基于特定的算法决定各单元的去与留。目前，常用的连续体结构拓扑优化方法包含：均匀化法（Homogenization Method）、相对密度法（Relative Denisity Method）（如SIMP法）、渐进结构优化方法（Evolutionary Structural Optimization Method）、独立连续映射方法（ICM Method）、水平集方法（Level Set Method）等，而在SolidWorks Simulation中便采用的是相对密度法也称之为变密度法中的SIMP法进行拓扑优化的计算。

关于SIMP法是由Bendsoe和Sigmund在Mlejnek等人提出相对密度法的基础之上提出的SIMP法，这种方法引入一种假想的相对密度在0-1之间的可变材料，假设设计材料的弹性模型与其密度的非线性关系，采用惩罚因子约束抑制介于0-1之间的单元，使中间密度值向0-1两端靠近，从而寻求具有某种结构特性的结构材料最佳分布形式，通常弹性模量与密度的关系表示为：

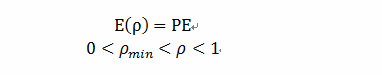
其中，E为弹性模量；P为惩罚因子，P>1；ρmin为材料为空的最小密度值，ρ为材料密度；

SIMP法的缺点

虽然能够有效地压缩中间密度，但是依然存在棋盘格现象和数值不稳定性现象，而且最终得到地拓扑结构不仅与惩罚因子P有关，还与初始有限元网格有关，但是这些缺点可以用其他方法进行修正。

而在SolidWorks Simulation中在进行每次迭代时，优化算例都会执行相关地灵敏度分析以评估材料密度变化对目标函数地影响，从而最大化刚度，而在灵敏度分析过程中，具有低权重材料密度因子的元素最终将失去其结构重要性，并将在进一步地迭代过程中被忽略，同时如果我们单独计算每个元素的灵敏度并且不考虑元素之间的连接性，则这可能会导致材料不连续以及会使得包络体与主几何体断开连接，这就是所谓的棋盘效应。为了减少棋盘效应，过滤方法将应用元素影响半径并求取各元素在其影响范围内的灵敏度的平均值。优化迭代也将继续，直到目标函数变化收敛且迭代达到其收敛条件。

申请SolidWorks Simulation正版试用

想了解 正版SOLIDWORKS？可以联系我们的 慧都客服~或者直接拨打023-68661681