拓扑学Topology笔记整理第二章几个重要的拓扑性质

盛煌注册

盛煌动态

拓扑学Topology笔记整理第二章几个重要的拓扑性质

发布时间：2024-05-26 09:04:01 点击量：

由于拓扑公理太弱，拓扑空间丧失了许多良好的性质。分离性和可数性常作为附加性质，来改善拓扑空间的性质，它们被称作分离公理和可数公理。

子集 $A$ 的邻域 $U$ 定义为 $A\\subset U^\\circ$ 。

$\\bf Def\\ (邻域系、邻域基)$

设 $x\\in X$ ，则 $x$ 所有邻域构成的集合记为 $\\mathscr N(x)$ ，称为 $x$ 的邻域系。设 $\\mathscr U\\subset\\mathscr N(x)$ 。若任意 $x$ 的邻域 $V$ ，都存在 $U\\in\\mathscr U$ 使得 $U\\subset V$ ，则称 $\\mathscr U$ 是 $x$ 的邻域基。

$\\bf e.g.$

$\\mathscr N(x)$ 是 $x$ 的邻域基；
$x$ 的全体开邻域构成 $x$ 的邻域基；
对于度量空间 $(X,d)$ ， $\\{B(x,\\varepsilon):\\varepsilon>0\\}$ 、 $\\{B(x,q):q>0,q\\in\\mathbb Q\\}$ 、 $\\{B(x,1/n):n\\in\\mathbb N^+\\}$ 都是 $x$ 的邻域基。

以下四条公理称为分离公理，其中的“邻域”可替换为“开领域”：

[ $T_1$ 公理] 任何两个不同点 $x,y$ ， $x$ 有邻域不含 $y$ ， $y$ 有邻域不含 $x$

[ $T_2$ 公理] 任何两个不同点有不相交的邻域

[ $T_3$ 公理] 任意一点与不含它的任一闭集有不相交的邻域

[ $T_4$ 公理] 任意两个不相交的闭集有不相交的邻域

其中 $T_2$ 公理是最重要的分离公理，满足 $T_2$ 的拓扑空间称为Hausdorff空间。

以下两条公理称为第一可数公理和第二可数公理：

[ $C_1$ 公理] 任一点都有可数的邻域基

[ $C_2$ 公理] 有可数的拓扑基

以下是一些分离公理的等价刻画。

$\\bf Prop\\ (分离公理的等价刻画)$

$X$ 满足 $T_1\\Leftrightarrow X$ 的单点（有限）子集都是闭集；

$\\it Proof$
$(\\Rightarrow)$ 设 $x\\in X$ ，下证 $\\overline{\\{x\\}}=\\{x\\}$ ，从而 $\\{x\\}$ 是闭集。事实上 $\\forall y\ eq x$ ， $y$ 有邻域不包含 $x$ ，于是 $y\ otin\\overline{\\{x\\}}$ ，从而 $\\overline{\\{x\\}}=\\{x\\}$ 。
$(\\Leftarrow)$ 设 $x\ eq y$ ，则 $\\{y\\}$ 是闭集， $X\\backslash\\{y\\}$ 是 $x$ 的不含 $y$ 的开邻域。同理 $Y\\backslash\\{x\\}$ 是 $y$ 的不含 $x$ 的开邻域，从而 $X$ 满足 $T_1$ 公理。

$X$ 满足 $T_2\\Leftrightarrow$ 任意的拓扑空间 $Y$ 和连续映射 $f:Y\ o X$ ，都有 $f$ 的图像 $G_f=\\{(y,f(y)):y\\in Y\\}$ 是乘积空间 $Y\ imes X$ 的闭子集；
$X$ 满足 $T_3\\Leftrightarrow X$ 的任意点 $x$ 和它的开邻域 $W$ ，存在 $x$ 的开邻域 $U$ 使得 $\\overline{U}\\subset W$ ；

$\\it Proof$
参考(4)的证明，同理可证。

$X$ 满足 $T_4\\Leftrightarrow X$ 的任意闭集 $A$ 和它的开邻域 $W$ ，存在 $A$ 的开邻域 $U$ 使得 $\\overline{U}\\subset W$ 。

$\\it Proof$
$(\\Rightarrow)$ 记 $B=W^c$ ，则 $A$ 与 $B$ 是不相交的闭集，由 $T_4$ 可知，存在 $A,B$ 的不相交的开邻域 $U,V$ 。此时 $\\overline U\\subset V^c\\subset B^c=W$ ，即 $U$ 就为所求。
$(\\Leftarrow)$ 设 $A$ 与 $B$ 是不相交的闭集，则 $B^c$ 是 $A$ 的开邻域，从而存在 $A$ 的开邻域 $U$ 使得 $\\overline{U}\\subset B^c$ 。记 $V=(\\overline U)^c$ ，则 $V$ 是开集，且 $B\\subset V$ ，并且 $U\\cap V=\\varnothing$ 。

$\\bf Thm\\ (T_4公理的另外两个等价条件)$

(Urysohn引理) $X$ 满足 $T_4\\Leftrightarrow$ 任意两个不相交的闭集 $A$ 和 $B$ ，存在连续函数 $f:X\ o\\mathbb E^1$ 在 $A$ 和 $B$ 上分别取值为 $0$ 和 $1$ ；
(Tietze扩张定理) $X$ 满足 $T_4\\Leftrightarrow$ 定义在 $X$ 的闭子集 $F$ 上的连续函数 $f:F\ o\\mathbb E^1$ 可以连续扩张到 $X$ 上，即存在连续函数； $g:X\ o\\mathbb E^1$ ，使得 $g_F=f$ 。

$\\bf Prop\\ (具有分离性的拓扑空间的性质)$

$X$ 满足 $T_1\\Rightarrow x$ 是 $A\\subset X$ 的聚点当且仅当 $x$ 的任意邻域与 $A$ 的交是无穷集；

$\\it Proof$
只证明必要性，充分性显然成立。设 $x$ 有开邻域 $U$ 使得 $U\\cap A$ 是有限集，记 $B=(U\\cap A)\\backslash\\{x\\}$ ，则 $B$ 是有限集从而是闭集，于是 $V=U\\backslash B$ 也是 $x$ 的开邻域，它满足 $V\\cap A\\backslash\\{x\\}=\\varnothing$ ，从而 $x\ otin\\overline A$ 。

$X$ 满足 $T_1\\Rightarrow$ 任意子集的导集是闭集；

$\\it Proof$
参考：如何证明Hausdorff空间中集合的导集为闭集？

Hausdorff空间中的序列的极限具有唯一性。

$\\it Proof$
设 $x_n\ o x$ ，若 $y\ eq x$ ，则 $x$ 和 $y$ 有不相交的邻域 $U_x$ 和 $U_y$ 。由定义有 $U_x$ 包含 $\\{x_n\\}$ 的几乎所有项，于是 $U_y$ 至多包含 $\\{x_n\\}$ 的有限项，从而不可能有 $x_n\ o y$ 。

下面的引理是研究可数拓扑基的常用技巧。

$\\bf Lemma$

若 $x$ 存在可数邻域基，则 $x$ 存在渐缩的可数邻域基 $\\{V_n\\}$ ，即 $\\forall m>n$ 有 $V_m\\subset V_n$ 。

$\\it Proof$
设 $\\{U_n\\}$ 是 $x$ 的可数邻域基，只需令 $V_n=\\bigcap_{i=1}^nU_i$ 即可。

$\\bf Prop\\ (C_1空间的性质)$

$X$ 满足 $C_1\\Rightarrow$ 设 $A\\subset X$ ，则 $x\\in\\overline A$ 当且仅当 $A$ 中存在收敛到 $x$ 的序列；
$X$ 满足 $C_1\\Rightarrow$ 映射 $f:X\ o Y$ 在 $x_0$ 连续当且仅当对于任意序列 $x_n\ o x$ 有 $f(x_n)\ o f(x)$ 。

$\\it Proof$
只证明必要性，充分性显然成立。取 $x$ 的可数邻域基 $\\{V_n\\}$ 使得 $\\forall m>n$ 有 $V _m\\subset V_n$ 。因为 $x\\in\\overline A$ ，所以对任意的 $n$ ， $V_n\\cap A\ eq\\varnothing$ ，取 $x_n\\in V_n\\cap A$ 。这样得到的 $\\{x_n\\}$ 收敛于 $x$ 。事实上任意 $x$ 的邻域 $U$ 必包含某个 $V_n$ ，从而 $\\forall m\\geq n$ 有 $x_m\\in V_m\\subset U$ 。
在第一章已经证明必要性，下证充分性。任给 $f(x_0)$ 的邻域 $V$ ，若 $f^{-1}(V)$ 不是 $x_0$ 的邻域，即 $x_0\\in((f^{-1}(V))^\\circ)^c=\\overline{(f^{-1}(V))^c}$ 。根据(1)，存在 $(f^{-1}(V))^c$ 中的序列 $x_n\ o x_0$ ，由条件有 $f(x_n)\ o f(x_0)$ 。从而存在 $N$ ，当 $n>N$ 时有 $f(x_n)\\in V$ ，即 $x_n\\in f^{-1}(V)$ ，矛盾！

$\\bf Def\\ (遗传性与可乘性)$

一种拓扑性质称为有遗传性，如果一个拓扑空间具有它蕴含子空间也具有它；
一种拓扑性质称为有可乘性，如果两个拓扑空间具有它蕴含乘积空间也具有它。

$\\bf Prop\\ (分离公理的遗传性和可乘性)$

公理 $T_1,T_2,T_3$ 具有遗传性和可乘性，但 $T_4$ 不具有遗传性和可乘性。

$\\it Proof$
$T_1$ 的遗传性和可乘性由其等价刻画很容易证明。
$(T_2的遗传性)$ 设 $a\ eq b\\in A\\subset X$ ，则存在 $U_a,U_b$ 分别是 $a,b$ 在 $X$ 中的开邻域，满足 $U_a\\cap U_b=\\varnothing$ 。令 $V_a=U_a\\cap A,V_b=U_b\\cap A$ ，则 $V_a,V_b$ 分别是 $a,b$ 在 $A$ 中的开邻域，满足 $V_a\\cap V_b=\\varnothing$ 。
$(T_2的可乘性)$ 设 $(x_1,y_1)\ eq(x_2,y_2)\\in X\ imes Y$ ，不妨设 $x_1\ eq x_2$ 。则存在 $U,V$ 是 $x_1,y_1$ 在 $X$ 的不相交的开邻域。则 $U\ imes Y$ 和 $V\ imes Y$ 就是 $(x_1,y_1),(x_2,y_2)$ 在 $X\ imes Y$ 的不相交的开邻域。
$(T_3的遗传性)$ 设 $a\\in A\\subset X$ ， $W$ 是 $A$ 中不含 $a$ 的闭集，则存在 $X$ 中的闭集 $F$ 使得 $W=F\\cap A$ 。由于 $a\ otin W$ 但 $a\\in A$ ，故 $a\ otin F$ 。由 $T_3$ 可知， $a,F$ 在 $X$ 存在不相交的开邻域 $U,V$ 。此时 $U\\cap A$ 和 $V\\cap A$ 分别是 $a$ 和 $W$ 在 $A$ 中的不相交的开邻域。
$(T_3的可乘性)$ 设 $(x,y)\\in X\ imes Y$ ， $W$ 是它的开邻域。由乘积拓扑的定义，存在 $U,V$ 分别是 $x,y$ 在 $X,Y$ 中的开邻域，使得 $U\ imes V\\subset W$ 。由 $T_3$ 可知，存在 $U_0,V_0$ 分别是 $x,y$ 在 $X,Y$ 中的开邻域，使得 $\\overline{U_0}\\subset U$ 以及 $\\overline{V_0}\\subset V$ 。则 $U_0\ imes V_0$ 是 $(x,y)$ 的开邻域，且 $\\overline{U_0\ imes V_0}=\\overline{U_0}\ imes\\overline{V_0}\\subset U\ imes V$ 。
$(T_4不具有遗传性)$ 设 $X=\\{a,b,c,d\\}$ 取拓扑 $\ au=\\{\\varnothing,X,\\{a\\},\\{a,b\\},\\{a,c\\},\\{a,b,c\\}\\}$ 。注意到 $X$ 的非空闭集都包含 $d$ ，从而都相交，因此 $X$ 是 $T_4$ 空间。它的子空间 $A=\\{a,b,c\\}$ 具有拓扑 $\ au_A=\\{\\varnothing,X,\\{a\\},\\{a,b\\},\\{a,c\\},\\{a,b,c\\}\\}$ 。它的两个非空闭集 $\\{b\\},\\{c\\}$ 没有不相交的开邻域，因此 $A$ 不是 $T_4$ 空间。

怎么举例说明T4分离公理不可乘且不可遗传？

$\\bf Prop\\ (可数公理的遗传性和可乘性)$

第一第二可数公理都具有遗传性和可乘性。

$\\bf Prop(可分性的遗传性和可乘性)$

可分性具有可乘性，但不具有遗传性。

$\\bf Prop$

$T_2$ 空间是 $T_1$ 空间；
满足 $T_1,T_3$ 的空间是 $T_2$ 空间；
满足 $T_1,T_4$ 的空间是 $T_3$ 空间。

$\\it Proof$
由 $T_1$ 的等价刻画和其余公理的定义易证。

$\\bf Thm$

度量空间 $(X,d)$ 满足 $T_i(i=1,2,3,4)$ 和 $C_1$ 。

$\\it Proof$
先证所有分离公理。按照定义容易证明 $(X,d)$ 满足 $T_1$ ，只需证 $T_4$ 也成立即可。事实上，设 $A,B$ 是不相交的非空闭集，则有 $d(x,A)+d(x,B)>0,\\forall x\\in X$ 。则连续函数 $f:X\ o\\mathbb E^1$ ， $f(x)=\\dfrac{d(x,A)}{d(x,A)+d(x,B)}$ 在 $A$ 和 $B$ 上分别取值为 $0$ 和 $1$ ，从而由Urysohn引理知 $T_4$ 成立。
$C_1$ 公理成立是因为 $\\{B(x,1/n):n\\in\\mathbb N^+\\}$ 是 $x$ 的可数邻域基。

$\\bf Prop$

$C_2$ 空间是 $C_1$ 空间；

$\\it Proof$
设 $X$ 有可数拓扑基 $\\{B_n\\}$ ，则 $\\{B_n:x\\in B_n\\}$ 是 $x$ 的可数邻域基。

$C_2$ 空间是可分空间；

$\\it Proof$
设 $X$ 有可数拓扑基 $\\{B_n\\}$ ，在每个 $B_n$ 中取一点构成集合 $A=\\{x_n\\}$ ，则 $A$ 是可数的稠密子集。事实上， $\\forall x\\in X$ ，设 $U$ 是 $x$ 的开邻域，由拓扑基的定义可知 $U$ 一定包含了某个 $B_n$ ，从而 $x_n\\in B_n\\subset U$ ，即 $U\\cap A\ eq\\varnothing$ ，从而 $x\\in\\overline A$ 。这就证明了 $\\overline A=X$ 。

可分的度量空间是 $C_2$ 空间。

$\\bf Thm$

欧氏空间 $\\mathbb E^n$ 是可分的度量空间，从而满足 $T_i(i=1,2,3,4)$ 和 $C_i(i=1,2)$ 。

$\\it Proof$
事实上 $A=\\{(x_1,\\dots,x_n):\\forall i,x_i\\in\\mathbb Q\\}$ 就是可数稠密子集。

$\\bf Prop$

所有收敛序列的极限唯一的 $C_1$ 空间是Hausdorff空间；

$\\it Proof$
若 $x\ eq y$ 没有不相交的开邻域。设 $\\{U_n\\},\\{V_n\\}$ 分别是它们的渐缩可数邻域基，则 $U_n\\cap V_n\ eq\\varnothing$ 。取 $x_n\\in U_n\\cap V_n$ ，则 $x_n$ 同时收敛到 $x,y$ 。

(Lindelof) 满足 $C_2,T_3$ 的空间是 $T_4$ 空间；
(Urysohn度量化定理) 满足 $T_i(i=1,2,3,4)$ 和 $C_i(i=1,2)$ 的空间是度量空间。

$\\bf e.g.\\ (一个不可分的度量空间，从而不满足C_2)$

设 $X$ 是不可数集合，规定度量 $d(x,y)=\\begin{cases}0&x=y\\\\ 1&x\ eq y \\end{cases}$ ，则 $(X,d)$ 是离散拓扑空间也是度量空间。它的任意子集 $A$ 是闭集，从而 $\\overline A=A$ 。因此它的所有可数子集都不是稠密子集，因此不可分，从而不是 $C_2$ 空间。

$\\bf e.g.\\ (一个满足T_4,C_{1,2},但不满足T_{1,2,3}的空间)$

$(\\mathbb R,\ au)(\ au=\\{(-\\infty,a):a\\in\\overline{\\mathbb R}\\})$ 中任意两个非空闭集都相交，因此它满足 $T_4$ 。按定义容易验证它不满足 $T_1,T_2,T_3$ 。 $\\mathscr B=\\{(-\\infty,q):q\\in\\mathbb Q\\}$ 是可数拓扑基，因此 $C_1,C_2$ 成立。更进一步我们得知它是可分空间。

$\\bf e.g.\\ (无穷集合的余有限拓扑)$

设 $X$ 是无穷集合，则 $(X,\ au_f)$ 具有如下性质：

满足 $T_1$ 、不满足 $T_{2,3,4}$ ；
可分；
互异点列收敛到任意点；
任何子集都紧致；
连通。

$\\it Proof$
因为 $(X,\ au_f)$ 的有限子集都是闭集，故 $T_1$ 成立。但任意的两个不同点 $x\ eq y$ 的开邻域一定相交，这是因为它们都是有限子集的余集。从而 $T_2$ 不成立，进而 $T_3,T_4$ 也不成立。
$X$ 的任意无穷子集 $A$ 都是稠密的，这是因为任意一点 $x$ 的开邻域都是有限子集的余集，必然与 $A$ 相交，因此 $x\\in\\overline A$ ，从而 $\\overline A=X$ 。因此 $X$ 的任意无穷子集都是可数稠密子集，从而 $X$ 可分。
设 $\\{x_n\\}$ 是互异点列，由于 $\\forall x\\in X$ 的开邻域的余集是有限集，它必然包含 $\\{x_n\\}$ 的几乎所有项，因此 $x_n\ o x$ 。
设 $A$ 是 $X$ 的非空子集， $\\mathscr{U}$ 是 $A$ 在 $X$ 中的开覆盖。取 $U_0\\in\\mathscr U$ ，由于 $U_0$ 是开集，则 $U_0^c$ 是有限集。 $A\\backslash U_0\\subset U_0^c$ 也是有限集，因此存在有限子覆盖 $\\{U_1,\\dots,U_n\\}$ 。于是有限子覆盖 $\\{U_0,U_1,\\dots,U_n\\}$ 覆盖了 $A$ 。
任何两个非空开集你一定相交。

$\\bf e.g.\\ (不可数集合的余可数拓扑)$

设 $X$ 是不可数集合，则 $(X,\ au_c)$ 具有如下性质：

满足 $T_1$ 、不满足 $T_{2,3,4}$ ；
不满足 $C_1$ ；
不可分；
$x_n\ o x\\Leftrightarrow \\{x_n\\}$ 几乎全部等于 $x$ ，即 $\\exist N,\\forall n>N,x_n=x$ ；
不紧致；
连通。

$\\it Proof$
与上例类似。
假设 $\\{U_n\\}$ 是 $x$ 的可数邻域基，任取 $y\ eq x$ ，则 $\\{y\\}^c$ 是 $x$ 的邻域，从而存在某个 $U_n\\subset\\{y\\}^c\\Leftrightarrow U_n^c\\supset\\{y\\}\\Leftrightarrow y\\in U_n^c$ 。从而就有 $\\{x\\}^c\\subset\\bigcup_{n}U_n^c$ 。注意到左边是一个不可数集合，右边是可数个可数集的并从而是可数集，矛盾！因此 $X$ 不满足 $C_1$ 。
$X$ 的任意可数子集 $A$ 都是闭集，因此 $\\overline A=A\\subsetneq X$ ，从而 $A$ 不是稠密子集。这说明 $X$ 没有可数的稠密子集，从而不可分。
充分性显然成立，只需证必要性。构造可数集 $A=\\{x_n:x_n\ eq x\\}$ ，则 $A$ 是闭集。由于 $x\ otin A$ ，所以 $A^c$ 是 $x$ 的开邻域，从而由于 $A^c$ 包含 $\\{x_n\\}$ 的几乎所有项。这说明 $\\{x_n\\}$ 几乎全部等于 $x$ 。
取 $X$ 的一个可数无限子集 $A=\\{a_0,a_1,\\dots\\}$ 。则 $\\mathscr{U}=\\{(X\\backslash A)\\cup\\{a_n\\}:n\\geq 0\\}$ 是 $X$ 的开覆盖，它没有有限子覆盖。
任何两个非空开集你一定相交。

$\\bf Def\\ (列紧性、紧致性)$

称拓扑空间 $X$ 是列紧的，如果 $X$ 的每个序列都有收敛的子序列；
称拓扑空间 $X$ 是紧致的，如果 $X$ 的每个开覆盖都有有限子覆盖；
如果拓扑空间的子集作为子空间是紧致(列紧)的，称它为紧致(列紧)子集。

$\\bf Prop\\ (列紧空间上连续函数最值定理)$

定义在列紧空间 $X$ 上的连续函数 $f:X\ o\\mathbb E^1$ 有界且能取最大最小值。

$\\it Proof$
若 $f$ 无界，则可以找到一个序列 $\\{x_n\\}\\subset X$ 使得 $f(x_n)\ o\\infty$ 。由列紧性， $\\{x_n\\}$ 有收敛子列，不妨其本身就收敛 $x_n\ o x_0$ ，则由连续性有 $f(x_n)\ o f(x_0)$ 与 $f(x_n)\ o\\infty$ 矛盾。设 $M=\\sup f(X)$ 。若 $M\ otin f(X)$ ，考虑函数 $g(x)=\\dfrac{1}{M-f(x)}$ 仍是 $X$ 上的连续函数。且由上确界的定义可以证明 $g$ 无界，从而导出矛盾。这就证明了 $f$ 能取到最大值 $M$ ，最小值同理可证。

$\\bf Prop$

对于 $C_1$ 空间，紧致 $\\Rightarrow$ 列紧。

$\\it Proof$
设 $\\{x_n\\}\\subset X$ ，不妨设它是互异点列，先证存在 $x\\in X$ 使得它的任意邻域都含有 $\\{x_n\\}$ 的无穷多项。反证法，若 $\\forall x\\in X$ ，存在 $x$ 的邻域 $U_x$ 只含有 $\\{x_n\\}$ 的有限项。注意到 $\\{U_x:x\\in X\\}$ 是一个开覆盖，由紧致性可知存在 $X$ 的有限子覆盖 $\\{U_{x_n}:n=1,2,\\dots,N\\}$ 。这样每个 $U_{x_n}$ 只含有 $\\{x_n\\}$ 的有限项，从而 $\\{x_n\\}=\\{x_n\\}\\cap\\bigcup_{n=i}^N U_{x_n}=\\bigcup_{n=i}^N(U_{x_n}\\cap\\{x_n\\})$ 是有限集，矛盾！
再证存在 $\\{x_n\\}$ 的子列以 $x$ 为极限。设 $\\{V_n\\}$ 是 $x$ 的渐缩的可数拓扑基，则每个 $V_n$ 都含有 $\\{x_n\\}$ 无穷多项。取 $x_{n_i}$ 为包含在 $V_i$ 中的那些项中的第 $i$ 个，则有 $n_{i+1}>n_i,\\forall i$ 。从而 $x_{n_i}\ o x,i\ o\\infty$ 。

度量空间都是 $C_1$ 空间，因此对于度量空间，紧致 $\\Rightarrow$ 列紧。

接下来我们证明对于度量空间，列紧 $\\Rightarrow$ 紧致。为此我们先引入“网”的概念。

$\\bf Def\\ (\\delta-网)$

设 $A$ 是度量空间 $X$ 的子集， $\\delta>0$ 是正数。若 $\\bigcup_{a\\in A}B(a,\\delta)=X$ ，则 $A$ 称为 $X$ 的 $\\delta$ -网。这等价于 $\\forall x\\in X,\\exists a\\in A$ 使得 $d(x,a)<\\delta$ ，也等价于 $\\forall x\\in X$ ， $d(x,A)<\\delta$ 。

$\\bf Def\\ (完全有界、有界)$

称度量空间 $X$ 完全有界，如果 $\\forall\\delta>0$ ， $X$ 总存在有限的 $\\delta$ -网；
称度量空间 $X$ 有界，如果 $\\exists M>0$ 使得 $\\forall x,y\\in X,d(x,y)<M$

显然完全有界蕴含了有界，事实上 $d(x,y)<2\\delta\\cdot|A_\\delta|$ ，其中 $|A_\\delta|$ 表示 $A_\\delta$ 的元素个数。

$\\bf Prop$

对于度量空间，完全有界 $\\Rightarrow C_2$ 。

$\\bf Prop$

对于度量空间，列紧 $\\Rightarrow$ 完全有界。

$\\it Proof$
若不然， $\\exists\\delta_0>0$ 使得 $X$ 的任意有限子集 $A$ 都不是 $\\delta$ -网，即 $\\exists x\\in X$ 使得 $d(x,A)\\geq\\delta_0$ 。任意取定 $x_1\\in X$ ，归纳假设 $x_1,\\dots,x_n$ 已经取好，将 $\\{x_1,\\dots,x_n\\}$ 看作上面的 $A$ ，则可再取 $x_{n+1}$ 使得 $d(x_{n+1},x_i)\\geq\\delta_0(1\\leq i\\leq n)$ 。这样得到的 $\\{x_n\\}$ 满足 $\\forall i\ eq j,d(x_i,x_j)\\geq\\delta_0$ ，因此它不可能有收敛子列，矛盾。

反之不对，例如 $(0,1)$ 作为欧式空间的子空间是完全有界的，显然它不列紧。

$\\bf Prop\\ (Lebesgue数)$

设 $\\mathscr U$ 是列紧度量空间 $(X,d)$ 的开覆盖，满足 $X\ otin\\mathscr U$ ，则 $\\varphi_{\\mathscr U}(x)=\\sup\\{d(x,U^c)\\mid U\\in\\mathscr U\\}$ 是 $X\ o\\mathbb E^1$ 的连续函数，它在 $X$ 上的最小值是一个正数，记作 $L(\\mathscr U)$ ，称为开覆盖 $\\mathscr U$ 的Lebesgue数。

$\\it Proof$
由于列紧的度量空间有界， $\\exists M>0$ 使得 $\\forall x,y\\in X,d(x,y)<M$ 。容易证明 $0<\\varphi_{\\mathscr U}(x)\\leq M,\\forall x\\in X$ ，因此 $\\varphi_{\\mathscr U}(x)$ 是良好定义的。
由于 $\\forall x,y\\in X$ ， $d(y,U^c)=\\inf_ad(y,a)\\leq d(x,y)+\\inf_ad(x,a)=d(x,y)+d(x,U^c)$ ，取上确界，则有 $\\varphi_{\\mathscr U}(x)\\leq d(x,y)+\\varphi_{\\mathscr U}(y)$ 。同理有 $\\varphi_{\\mathscr U}(y)\\leq d(x,y)+\\varphi_{\\mathscr U}(x)$ 。因此 $|\\varphi_{\\mathscr U}(x)-\\varphi_{\\mathscr U}(y)|\\leq d(x,y)$ ，从而 $\\varphi_{\\mathscr U}(x)$ 连续。由连续函数在列紧空间的最值定理可知 $L(\\mathscr U)>0$ 是良好定义的。

$\\bf Prop\\ (Lebesgue引理)$

设 $\\mathscr U$ 是列紧度量空间 $(X,d)$ 的开覆盖，则任取 $0<\\delta<L(\\mathscr U)$ 和 $x\\in X$ ，存在 $U\\in\\mathscr U$ 使得 $B(x,\\delta)\\subset U$ 。

$\\it Proof$
$\\forall x\\in X$ ，则 $\\delta<L(\\mathscr U)\\leq\\varphi_{\\mathscr U}(x)=\\sup\\{d(x,U^c)\\mid U\\in\\mathscr U\\}$ ，因此由上确界的定义，存在 $U\\in\\mathscr U$ 使得 $d(x,U^c)>\\delta$ ，从而 $B(x,\\delta)\\subset U$ 。

$\\bf Prop$

对于度量空间，列紧 $\\Rightarrow$ 紧致。

$\\it Proof$
设 $\\mathscr U$ 是列紧度量空间 $(X,d)$ 的开覆盖，下证它有有限子覆盖。取 $0<\\delta<L(\\mathscr U)$ ，由列紧度量空间的全有界性，存在有限 $\\delta$ -网 $A=\\{a_1,\\dots,a_n\\}$ ，于是 $\\bigcup_{i=1}^nB(a_i,\\delta)=X$ 。由Lebesgue引理，对每个 $B(a_i,\\delta)$ ，都存在 $U_i\\in\\mathscr U$ 使得 $B(a_i,\\delta)\\subset U_i$ ，从而 $\\{U_1,\\dots,U_n\\}$ 是有限子覆盖。

由此我们就得到了此部分的主要结论

$\\bf Thm\\ 1$

设 $X$ 是度量空间，则 $A\\subset X$ 是紧致子集 $\\Leftrightarrow$ 是列紧子集 $\\Rightarrow$ 是有界闭集

$\\it Proof$
第一个等价前面已经证明。若 $A$ 是列紧子集，前面已经证明 $A$ 有界。任给 $x\\in \\overline A$ ，由 $C_1$ 空间的性质知，存在 $A$ 中的序列 $\\{x_n\\}$ 收敛到 $x$ 。由列紧性可知 $\\{x_n\\}$ 有收敛子列 $x_{n_k}\ o x_0\\in A$ ，又因为 $x_{n_k}\ o x$ 以及Hausdorff空间中极限的唯一性， $x=x_0\\in A$ 。这就证明了 $\\overline A\\subset A$ ，从而 $A$ 是 $X$ 的有界闭集。

$\\bf Rmk$

这里 $A$ 的闭集可以由后面的命题：Hausdorff空间的紧致子集是闭集直接得到；
$A$ 是 $X$ 的有界闭集 $\ ot\\Rightarrow A$ 作为子空间列紧：

反例1：无穷集合的离散拓扑是自身的有界闭集，它的每一个点放在一起构成一个没有有限子覆盖的开覆盖。

反例2：Hilbert空间 $E^\\omega$ 的单位正交基 $\\{e_i\\}$ 构成的子集是有界闭集。但它作为序列满足 $d(e_i,e_j)=\\sqrt2(i\ eq j)$ ，因此不可能有收敛的子列。

子空间的开覆盖可以在更大的空间中考虑。具体来说，若 $X$ 中的一个开集族 $\\mathscr U$ 如果满足 $A\\subset\\bigcup_{U\\in\\mathscr U}U$ ，则称 $\\mathscr U$ 是 $A$ 在 $X$ 中的开覆盖。

$\\bf Prop$

$A$ 是 $X$ 的紧致子集 $\\Leftrightarrow A$ 在 $X$ 中的任何开覆盖都有有限子覆盖。

$\\bf Prop(紧致空间的闭集是紧致子集)$

设 $X$ 是紧致空间， $A$ 是闭集，则 $A$ 是紧致子集。

$\\it Proof$
设 $X$ 是紧致空间， $A$ 是闭集。设 $\\mathscr U$ 是 $A$ 在 $X$ 中的开覆盖，因为 $A^c$ 是开集，所以 $\\mathscr U\\cup\\{A^c\\}$ 是 $X$ 的开覆盖。由于 $X$ 紧致，存在有限开覆盖 $\\{U_1,\\dots,U_n,A^c\\}$ ，则 $\\{U_1,\\dots,U_n\\}$ 是 $A$ 在 $X$ 中的开覆盖。

$\\bf Thm\\ 2$

欧氏空间的子集 $A\\subset\\mathbb R^n$ 是紧致子集 $\\Leftrightarrow$ 是列紧子集 $\\Leftrightarrow$ 是有界闭集。

$\\it Proof$
根据Thm1，只需证明若 $A$ 是有界闭集，则 $A$ 是紧致子集即可。事实上，由于 $A$ 是有界闭集，从而 $A$ 可以包含于某个闭矩体。由数学分析的知识可知闭矩体都是紧致的，因此由上面的命题，它的闭子集 $A$ 也是紧致的。

$\\bf Prop\\ (连续映射保持紧致)$

设 $f:X\ o Y$ 是连续映射，则 $f$ 把 $X$ 的紧致子集映成 $Y$ 的紧致子集。

$\\it Proof$
设 $A\\subset X$ 是紧致子集，下证 $B=f(A)$ 是 $Y$ 的紧致子集。设 $\\mathscr U$ 是 $B$ 在 $Y$ 中的开覆盖，则 $\\{f^{-1}(U):U\\in\\mathscr U\\}$ 是 $A$ 在 $X$ 中的开覆盖，从而有有限子覆盖使得 $A\\subset\\bigcup_{i=1}^n f^{-1}(U_i)$ ，则 $B=f(A)\\subset f(\\bigcup_{i=1}^n f^{-1}(U_i))=\\bigcup_{i=1}^n f(f^{-1}(U_i))\\subset\\bigcup_{i=1}^n U_i$ ，这就是说 $\\{U_1,\\dots,U_n\\}$ 是 $B$ 在 $Y$ 中的有限子覆盖。

$\\bf Prop\\ (紧致空间上连续函数最值定理)$

定义在紧致空间 $X$ 上的连续函数 $f:X\ o\\mathbb E^1$ 有界且能取最大最小值。

$\\it Proof$
由上面的命题可知 $f(X)$ 是度量空间 $\\mathbb E^1$ 中的紧致子集，从而是有界闭集，从而 $f(X)$ 包含了它的上下确界。因此 $f:X\ o\\mathbb E^1$ 有界且能取最大最小值。

$\\bf Prop$

设 $A$ 是Hausdorff空间 $X$ 的紧致子集， $x\ otin A$ ，则 $x$ 与 $A$ 有不相交的开邻域；
设 $A,B$ 是Hausdorff空间 $X$ 的不相交的紧致子集，则 $A,B$ 有不相交的开邻域。

$\\it Proof$
$\\forall y\\in A$ ，则 $x\ eq y$ ，由 $T_2$ 公理， $x,y$ 有不相交的开邻域 $U_y,V_y$ 。这样 $\\{V_y:y\\in A\\}$ 是 $A$ 的开覆盖，有有限子覆盖 $\\{V_{y_1},\\dots,V_{y_n}\\}$ 。令 $V=\\bigcup_{i=1}^n V_{y_i}$ 和 $U=\\bigcap_{i=1}^n U_{y_i}$ ，则它们分别是 $A$ 和 $x$ 的开邻域， $U\\cap V=\\varnothing$ 。
$\\forall x\\in B$ ，则 $x$ 与 $A$ 有不相交的开邻域 $U_x,V_x$ 。这样 $\\{U_x:x\\in B\\}$ 是 $A$ 的开覆盖，有有限子覆盖 $\\{U_{x_1},\\dots,U_{x_n}\\}$ 。令 $U=\\bigcup_{i=1}^n U_{x_i}$ 和 $V=\\bigcap_{i=1}^n V_{x_i}$ ，则它们分别是 $A$ 和 $B$ 的开邻域， $U\\cap V=\\varnothing$ 。

$\\bf Prop\\ (Hausdorff空间的紧致子集是闭集)$

设 $A$ 是Hausdorff空间 $X$ 的紧致子集，则 $A$ 是闭集。

$\\it Proof$
$\\forall x\ otin A$ ， $x$ 有邻域与 $A$ 不相交，因此 $x\ otin\\overline A$ ，这说明 $\\overline A=A$ 。

若去掉Hausdorff空间的条件，一般不对：

反例1：无穷集合的余有限拓扑的任何子集都是紧致子集（参看§1.6）它的无穷真子集紧致但非闭。

反例2： $X=\\{a,b\\}$ 取拓扑 $\ au=\\{\\varnothing,X,\\{a\\}\\}$ 。有限的拓扑空间总是紧致的，它的紧致子集 $A=\\{a\\}$ 不是闭集。

$\\bf Rmk$

紧致Hausdorff空间的紧致子集等价于闭集。

$\\bf Prop$

紧致Hausdorff空间满足 $T_3,T_4$ 公理。

$\\it Proof$
只需证满足 $T_4$ 公理。设 $A,B$ 是紧致Hausdorff空间 $X$ 的不相交的闭集，则由上述命题可知 $A,B$ 是不相交的紧致子集，从而有不相交的开邻域。

$\\bf Thm\\ 3\\ (紧致空间到Hausdorff 空间的连续映射是闭映射)$

设 $X$ 是紧致空间， $Y$ 是Hausdorff空间， $f:X\ o Y$ 是连续映射，则 $f$ 是闭映射；
特别地，如果 $f$ 是连续的双射，则 $f$ 是同胚映射。

$\\it Proof$
设 $A$ 是紧致空间 $X$ 的闭集，则由上面的命题可知 $A$ 是紧致子集，因此 $f(A)$ 是 $Y$ 的紧致子集，从而是闭集。从而 $f$ 把闭集映成闭集，从而是闭映射。

紧致性没有遗传性，本小节来证明其有可乘性。

$\\bf Prop$

设 $A$ 是 $X$ 的紧致子集， $y\\in Y$ ，在乘积空间中 $W$ 是 $A\ imes\\{y\\}$ 的邻域，则存在 $A$ 和 $y$ 的开邻域使得 $U\ imes V\\subset W$ 。

$\\it Proof$
$\\forall x\\in A$ ，则 $(x,y)$ 是 $W$ 的内点，从而存在 $x$ 和 $y$ 的开邻域 $U_x$ 和 $U_y$ 使得 $U_x\ imes U_y\\subset W$ 。注意到 $\\{U_x:x\\in X\\}$ 是 $A$ 的开覆盖，由紧致性，存在有限子覆盖 $\\{U_{x_1},\\dots,U_{x_n}\\}$ 。则 $U=\\bigcup_{i=1}^nU_{x_i}$ 和 $V=\\bigcap_{i=1}^nV_{x_i}$ 分别是 $A$ 和 $y$ 的开邻域，并且满足 $U\ imes V=\\bigcup_{i=1}^n(U_{x_i}\ imes V_{x_i})\\subset W$ 。

$\\bf Prop\\ (紧致性具有可乘性)$

若 $X,Y$ 紧致，则有 $X\ imes Y$ 也紧致。

$\\it Proof$
设 $\\mathscr U$ 是 $X\ imes Y$ 的开覆盖。 $\\forall y\\in Y$ ，由于 $X\ imes\\{y\\}\\cong X$ ，从而是紧致的。 $\\mathscr U$ 是它在 $X\ imes Y$ 中的开覆盖，从而存在有限子覆盖，设这个有限子覆盖的并集是 $W_y$ ，则 $X\ imes\\{y\\}\\subset W_y$ 。由上述命题可知，存在 $y$ 的开邻域 $V_y$ 使得 $X\ imes V_y\\subset W_y$ 。于是 $\\{V_y:y\\in Y\\}$ 是 $Y$ 的开覆盖，由紧致性，存在有限子覆盖 $\\{V_{y_1},\\dots,V_{y_n}\\}$ 。则 $X\ imes Y=\\bigcup_{i=1}^n(X\ imes Y_{y_i})\\subset\\bigcup_{i=1}^nW_{y_i}$ 被 $\\mathscr U$ 中有限个成员覆盖了。

设 $(X,\ au)$ 是非紧致的Hausdorff空间。在 $X$ 中添加一个元素 $\\infty$ 得到集合 $X_\\ast=X\\cup\\{\\infty\\}$ 。规定 $\ au_\\ast=\ au\\cup\\{X_\\ast\\}\\cup\\{X_\\ast\\backslash K:K是X的紧致子集\\}$ ，则

$\ au_\\ast$ 是 $X_\\ast$ 上的拓扑，且 $X$ 作为 $(X_\\ast,\ au_\\ast)$ 的子集的子空间拓扑就是 $\ au$ ；
$X$ 是 $(X_\\ast,\ au_\\ast)$ 的稠密子集；
$(X_\\ast,\ au_\\ast)$ 是紧致的，称为 $(X,\ au)$ 的一点紧致化。

$\\bf Recall$

称 $(R,+,0,\ imes,1)$ 是交换幺环，如果：

$(R,+,0)$ 是交换群；
$(R,\ imes,1)$ 满足交换律 $ab=ba$ 和结合律 $(ab)c=a(bc)$ ；
满足分配率 $a(b+c)=ab+ac$ 。

称 $I$ 是 $R$ 的理想，如果：

$(I,+,0)$ 是 $R$ 的子群；
$\\forall r\\in I,s\\in R\\Rightarrow rs\\in I$ 。

称 $P$ 是 $R$ 的素理想，如果：

$P$ 是 $R$ 的真理想，即 $P\ eq R$ ；
$\\forall r,s\\in R,rs\\in P\\Rightarrow r\\in P$ 或 $s\\in P$ 。

对于两个理想 $I_1,I_2$ ，有

$I_1+I_2=\\{r_1+r_2:r_i\\in I_i\\}$ ；
无穷个理想的和 $\\sum_\\alpha I_\\alpha=\\{\\sum_{有限个}r_\\alpha:r_\\alpha\\in I_\\alpha\\}$ ；
$I_1I_2=\\{\\sum_{有限个}r_{1,\\alpha}r_{2,\\alpha}:r_{i,\\alpha}\\in I_i\\}\\subset I_1\\cap I_2$ 。

$\\bf Def\\ (谱)$

$R$ 的全体素理想的集合称为谱(Spectrum)，记作 $\\mathrm{Spec}(R):=\\{P:P是素理想\\}$ 。

$\\bf e.g.$

$\\mathbb Z$ 在整数的加法和乘法下是交换幺环， $m\\mathbb Z$ 是一个理想， $p\\mathbb Z$ 是一个素理想， $\\mathbb Z$ 的谱是 $\\mathrm{Spec}(\\mathbb Z)=\\{p\\mathbb Z:p是素数\\}\\cup\\{\\{0\\}\\}$ 。

$\\bf Thm\\ (Zariski拓扑)$

设 $R$ 是交换幺环。对于任意的理想 $I$ ，定义 $V(I):=\\{P\\in\\mathrm{Spec}(R):I\\subset P\\}\\subset\\mathrm{Spec}(R)$ 作为闭子集，从而得到子集族 $\ au=\\{\\mathrm{Spec}(R)\\backslash V(I):I是理想\\}$ 。则 $\ au$ 是 $\\mathrm{Spec}(R)$ 的拓扑，称为Zariski拓扑

$\\it Proof$
$\\varnothing=V(R)$ ，这是因为素理想都是真理想，不可能包含 $R$ 。 $\\mathrm{Spec}(R)=V(\\{0\\})$ ，这是因为所有理想都包含零元。
利用下面的引理可以证明，任意闭集的交是闭集以及两个闭集的并是闭集。

$\\bf Lemma$

$\\bigcap_\\alpha V(I_\\alpha)=V(\\sum_\\alpha I_\\alpha)$ ；
$V(I_1)\\cup V(I_2)=V(I_1I_2)$ 。

$\\it Proof$
$\\forall P\\in\\bigcap_\\alpha V(I_\\alpha)$ ，则 $\\forall\\alpha,P\\in V(I_\\alpha)$ ，即 $\\forall\\alpha,I_\\alpha\\subset P$ 。注意到同时包含全体 $I_\\alpha$ 的最小的理想是 $\\sum_\\alpha I_\\alpha$ ，所以 $\\sum_\\alpha I_\\alpha\\subset P$ ，所以 $P\\in V(\\sum_\\alpha I_\\alpha)$ ，这就证明了 $LHS\\subset RHS$ 。另一方面， $\\forall P\\in V(\\sum_\\alpha I_\\alpha)$ ，则 $\\sum_\\alpha I_\\alpha\\subset P$ 。由于 $\\forall\\alpha, I_\\alpha\\subset\\sum_\\alpha I_\\alpha\\subset P$ ，所以也有 $\\forall P\\in\\bigcap_\\alpha V(I_\\alpha)$ 。这就证明了 $RHS\\subset LHS$ 。
$\\forall P\\in V(I_1)\\cup V(I_2)$ ，则 $I_i\\subset P$ 。由于 $I_1I_2\\subset I_1\\subset P$ ，从而 $P\\in V(I_1I_2)$ ，这就证明了 $LHS\\subset RHS$ 。另一方面， $\\forall P\\in V(I_1I_2)$ ，则 $I_1I_2\\subset P$ 。若 $I_1\ ot\\subset P$ ，则 $\\exists r_1\\in I_1$ 使得 $r_1\ otin P$ 。 $\\forall r_2\\in I_2$ 则 $r_1r_2\\in I_1I_2\\subset P$ 。由于 $P$ 是素理想， $r_2\\in P$ ，从而 $I_2\\subset P$ 。这就证明了 $I_2\\subset P$ 。即 $P\\in V(I_1)\\cup V(I_2)$ 。这就证明了 $RHS\\subset LHS$ 。

$\\bf Prop(Zariski拓扑的性质)$

$(\\mathrm{Spec}(R),\ au)$ 非Hausdorff空间；
$(\\mathrm{Spec}(R),\ au)$ 是紧致空间。

$\\it Proof$
设 $P_1\ eq P_2$ 是 $\\mathrm{Spec}(R)$ 中的元素，假设它们存在不相交的开邻域 $U_1$ 和 $U_2$ 。则 $U_1\\cap U_2=\\varnothing\\Leftrightarrow U_1^c\\cup U_2^c=\\mathrm{Spec}(R)$ 。由于 $U_i^c$ 是闭集，可设 $U_i^c=V(I_i)$ ，从而 $\\mathrm{Spec}(R)=U_1^c\\cup U_2^c=V(I_1)\\cup V(I_2)=V(I_1I_2)$ 。从而有 $\\{0\\}\\in V(I_1I_2)$ ，这说明 $I_1I_2\\subset\\{0\\}\\Rightarrow I_1I_2=\\{0\\}$ 。但是 $U_i\ eq\\varnothing\\Rightarrow U_i^c\ eq\\mathrm{Spec}(R)\\Rightarrow I_i\ eq \\{0\\}$ ，从而 $I_1I_2\ eq\\{0\\}$ ，矛盾！
设 $\\mathscr U=\\{U_\\alpha\\}$ 是 $\\mathrm{Spec}(R)$ 的开覆盖，即 $\\bigcup_\\alpha U_\\alpha=\\mathrm{Spec}(R)\\Leftrightarrow \\bigcap_\\alpha U_\\alpha^c=\\varnothing$ 。设 $U_\\alpha^c=V(I_\\alpha)$ ，从而 $\\varnothing=\\bigcap_\\alpha V(I_\\alpha)=V(\\sum_\\alpha I_\\alpha)$ 。我们断言 $\\sum_\\alpha I_\\alpha=R$ 。这是因为若 $\\sum_\\alpha I_\\alpha\\subsetneq R$ 是真理想，则 $\\sum_\\alpha I_\\alpha$ 一定包含于一个极大理想 $M$ 当中，而极大理想都是素理想，所以 $M\\in V(\\sum_\\alpha I_\\alpha)\\Rightarrow V(\\sum_\\alpha I_\\alpha)\ eq\\varnothing$ ，矛盾！ $1\\in R=\\sum_\\alpha I_\\alpha\\Rightarrow$ 存在有限个 $r_i\\in I_i(1\\leq i\\leq N)$ 使得 $\\sum_{i=1}^N r_i=1$ ，从而 $1\\in\\sum_{i=1}^N I_i\\Rightarrow \\sum_{i=1}^N I_i=R$ ，这是因为包含单位元的理想一定是环本身。从而得到了 $\\mathrm{Spec}(R)$ 的有限开覆盖 $\\mathrm{Spec}(R)\\backslash V(I_i)(1\\leq i\\leq N)$ 。

$\\bf Def\\ (局部紧致)$

如果 $\\forall x\\in X$ 都有紧致邻域，则称 $X$ 是局部紧致空间。

下面的命题留作备用，不作为考试内容。

$\\bf Prop$

设 $X$ 是局部紧致的Hausdorff空间，则

$X$ 满足 $T_3$ 公理；
$X$ 中每一点的所有紧致邻域构成邻域基，即对于 $\\forall x\\in X$ 的任意邻域 $U$ 都存在 $X$ 的紧致邻域 $V\\subset U$ ；
$X$ 的开集也是局部紧致的。

$\\bf Def\\ (连通)$

如果拓扑空间 $X$ 不能分解为两个非空开集的并，则称 $X$ 是连通空间。若 $A\\subset X$ 作为子空间是连通空间，则称 $A$ 是 $X$ 的连通子集。

容易证明 $X$ 连通等价于：

$X$ 不能分解为两个非空闭集的并；
$X$ 没有既开又闭的非空真子集；
$X$ 的既开又闭自己只有 $X$ 和 $\\varnothing$ 。

$\\bf e.g.$

设 $X$ 是无穷集合，则 $(X,\ au_f)$ 是连通空间；
设 $X$ 是不可数集合，则 $(X,\ au_c)$ 是连通空间；
设 $R$ 是交换幺环，则Zariski拓扑 $(\\mathrm{Spec}(R),\ au)$ 是连通空间。

$\\it Proof$
因为它们的任意两个非空开集一定相交。

$\\bf e.g.$

$\\mathbb{E^1}$ 是连通空间。

$\\it Proof$
设 $A\\subsetneq\\mathbb{E^1}$ 是非空真闭集，下证 $A$ 不是开集。不妨设 $0\ otin A$ 但 $A$ 但含有正数，由确界原理可知 $a=\\inf(A\\cap\\mathbb{R^+})\\in\\mathbb{R}$ 。由于 $A$ 是闭集，我们有 $a\\in A$ 。但是由下确界的性质可知 $(0,a)\\cap A=\\varnothing$ ，从而 $a\ otin A^\\circ$ ，这说明 $A$ 不是开集。

$\\bf Prop\\ (连续映射保持连通)$

设 $f: X\ o Y$ 是连续映射，则 $f$ 把 $X$ 的连通子集映成 $Y$ 的连通子集。

$\\it Proof$
设 $A\\subset X$ 是连通子集，下证 $B=f(A)$ 是 $Y$ 的连通子集。设 $V$ 是 $B$ 的既开又闭非空子集，则 $f|_A^{-1}(V)$ 是 $A$ 中的既开又闭非空子集。由 $X$ 的连通性可知 $f|_A^{-1}(V)=A$ ，从而 $V=f_A(A)=B$ 。这说明 $B$ 中没有既开又闭的非空真子集，从而连通。

再由同胚的定义容易证明，连通性是同胚不变量。

$\\bf e.g.$

$S^1=\\{(x,y)\\subset\\mathbb{E^2}:x^2+y^2=1\\}$ 是连通空间。

$\\it Proof$
$f(x)=(\\cos x,\\sin y)$ 是 $\\mathbb{E^1}\ o S^1$ 的连续函数。

$\\bf e.g.$

$\\mathbb{E^1}$ 的凸子集称为区间（即 $\\forall a,b\\in A(a<b)\\Rightarrow[a,b]\\subset A$ ）。设 $A\\subset\\mathbb{E^1}$ ，则 $A$ 连通 $\\Leftrightarrow A$ 是区间。

$\\it Proof$
$(\\Rightarrow)$ 若 $A$ 不是区间，则存在实数 $a<c<b$ 使得 $a,b\\in A$ 但 $c\ otin A$ 。则 $A=(A\\cap(-\\infty,c))\\cup(A\\cap(c,+\\infty))$ ，从而 $A$ 不连通。
$(\\Leftarrow)$ 若 $A$ 是区间，即 $A$ 是凸子集，容易证明 $A$ 是下列几种形式之一： $(a,b),[a,b],[a,b),(a,b]$ ，其中 $a,b\\in\\overline{\\mathbb{R}},a<b$ ，对于 $[a,b]$ 也允许 $a=b$ 。 $(a,b)\\cong\\mathbb{E^1}$ 连通。 $f(x)=|x|$ 是 $\\mathbb{E^1}\ o[0,+\\infty)$ 的连续满射，因此 $[a,b)\\cong(a,b]\\cong[0,\\infty)$ 连通。 $g(x)=\\frac{1}{2}(|x-a|-|x-b|-|a|+|b|)$ 是 $\\mathbb{E^1}\ o[a,b]$ 的连续满射，因此 $[a,b]$ 连通。

$\\bf Prop$

定义在连通空间 $X$ 上的连续函数 $f:X\ o\\mathbb{E^1}$ 具有介值性，即其像集是区间。

下面的引理在证明连通性时十分好用。

$\\bf Lemma$

设 $X_0$ 是 $X$ 的既开又闭子集， $A$ 是 $X$ 的连通子集，则或者 $A\\cap X_0=\\varnothing$ ，或者 $A\\subset X_0$ 。

$\\it Proof$
注意到 $X_0$ 是 $X$ 的既开又闭非空子集，则 $A\\cap X_0$ 是 $A$ 的既开又闭子集。

$\\bf Prop$

若 $X$ 有连通稠密子集，则 $X$ 连通。

$\\it Proof$
设 $A$ 是 $X$ 的连通稠密子集。设 $X_0$ 是 $X$ 的既开又闭非空子集。因为 $A$ 稠密，由稠密子集的充要条件， $X$ 的任意非空开集与 $A$ 相交非空，由引理可知 $A\\subset X_0$ 。于是 $X=\\overline{A}\\subset\\overline{X_0}=X_0\\Rightarrow X=X_0$ 。

$\\bf Cor$

若 $A$ 是 $X$ 的连通子集，并且 $A\\subset Y\\subset\\overline{A}$ ，则 $Y$ 连通。利用这个推论，也可以证明 $\\mathbb{E^1}$ 中区间都连通。

$\\bf e.g.\\ (拓扑学家的正弦曲线)$

设 $A=\\left\\{\\left(x,\\sin\\dfrac{1}{x}\\right):x\\in(0,1)\\right\\}$ ， $B=\\{0\\}\ imes[-1,1]$ ， $X=A\\cup B$ ，则 $X$ 连通。

$\\it Proof$
首先由于 $A\\cong (0,1)$ ， $A$ 是连通子集。又由于 $\\overline{A}=X$ ，所以 $A$ 是 $X$ 的连通稠密子集，由上述命题可知 $X$ 稠密。

$\\bf Thm$

若存在 $X$ 的连通覆盖（每个成员都是连通子集） $\\mathscr{U}$ 和连通子集 $A$ 使得 $\\forall U\\in\\mathscr{U},A\\cap U\ eq\\varnothing$ ，则 $X$ 连通。

$\\it Proof$
设 $X_0$ 是 $X$ 的既开又闭子集，下证 $X_0=X$ 或 $\\varnothing$ 。事实上，由引理可知 $A\\cap X_0=\\varnothing$ 或 $A\\subset X_0$ 成立。
若 $A\\cap X_0=\\varnothing$ 。 $\\forall U\\in\\mathscr{U},A\\cap U\ eq\\varnothing$ ，从而有 $U\ ot\\subset X_0$ ，再次利用引理就有 $U\\cap X_0=\\varnothing$ 。则 $X_0=\\bigcup_{U\\in\\mathscr{U}}U\\cap X_0=\\varnothing$ 。
若 $A\\subset X_0$ 。则类似有 $\\forall U\\in\\mathscr{U},U\\cap X_0\ eq\\varnothing$ ，由引理有 $U\\subset X_0$ 。从而 $X=\\bigcup_{U\\in\\mathscr{U}}U\\subset X_0\\Rightarrow X_0=X$ 。

由定理可知，两个连通子集的有交并是连通子集。

利用这个定理，我们可以证明如下结论。

$\\bf e.g.\\ (欧式空间和球面的连通性)$

$\\mathbb{E^n}$ 是连通空间；
$S^n$ 是连通空间。

$\\it Proof$
只证 $n=2$ ，其余可用归纳法证明。由于 $\\{\\{x\\}\ imes\\mathbb{R}:x\\in\\mathbb{R}\\}$ 是 $\\mathbb{E^2}$ 的连通覆盖，它的每一个成员与连通子集 $\\mathbb{R}\ imes\\{0\\}$ 相交非空，由定理即证。
由于 $S^n\\backslash\\{N\\}\\cong\\mathbb{E^n}$ 是连通子集，容易证明它也是稠密的，所以 $S^n$ 连通。

$\\bf Prop\\ (连通性的可乘性)$

连通性具有可乘性。

$\\it Proof$
设 $X,Y$ 都是连通空间。取 $y_0\\in Y$ ，则 $\\{\\{x\\}\ imes Y:x\\in X\\}$ 是 $X\ imes Y$ 的连通覆盖，它的每一个成员与连通子集 $X\ imes\\{y_0\\}$ 相交非空，由定理即证。

$\\bf Def\\ (连通分支)$

设 $A\\subset X$ 是连通子集，若对于任意包含 $A$ 的连通子集 $B\\supset A$ 都有 $B=A$ ，则称 $A$ 是 $X$ 的一个连通分支。换句话说连通分支就是极大连通子集。

$\\bf Prop$

$X$ 的任意非空连通子集包含于一个唯一的连通分支中；
$X$ 可以唯一地分解为连通分支的无交并；
连通分支是闭集。

$\\it Proof$
设 $A$ 是非空连通子集，令 $\\mathscr{F}=\\{F\\subset X:F连通,F\\cap A\ eq\\varnothing\\}$ 。因为至少 $A\\in\\mathscr{F}$ ， $\\mathscr{F}$ 非空。令 $Y=\\bigcup_{F\\in\\mathscr{F}}F$ ，容易证明 $Y$ 就是唯一的连通分支。
由于 $X$ 的每一点作为子空间都是连通的， $x$ 包含于唯一的连通分支中。
这是因为设 $Y$ 是连通分支，则 $\\overline Y$ 也连通。

拓扑空间 $X$ 的连通分支无交分解诱导了 $X$ 上的一个等价关系： $x\\sim y\\Leftrightarrow x,y$ 属于同一个连通分支。

$\\bf Def\\ (道路)$

拓扑空间 $X$ 上的一条道路指的是一个连续映射 $a:I\ o X$ 。 $a(0)$ 和 $a(1)$ 分别称为起点和终点。特别地，常值函数 $e_x:I\ o\\{x\\}\\subset X$ 称为一个点道路。起点和终点相同的道路称为一个闭路。点道路是闭路。定义道路的运算如下：

设 $a:I\ o X$ 是道路，定义 $a$ 的逆为 $\\overline{a}(t)=a(1-t)$ ；
设道路 $a,b$ 满足 $a(1)=b(0)$ ，定义它们的乘积为 $ab(t)=\\begin{cases}a(2t)&0\\leq t\\leq 1/2\\\\b(2t-1)&1/2\\leq t\\leq 1\\end{cases}$ 。由粘连定理可知 $ab$ 连续，从而是道路。

$\\bf Def\\ (道路连通)$

如果 $\\forall x,y\\in X$ 都存在分别以 $x,y$ 为起点和终点的道路，则称 $X$ 是道路连通空间。若 $A\\subset X$ 作为子空间是道路连通空间，则称 $A$ 是 $X$ 的道路连通子集。

$\\bf e.g.$

显然 $\\mathbb{E^n}$ 中的凸集是道路连通的。

$\\bf e.g.\\ (拓扑学家的正弦曲线)$

$X=A\\cup B=\\left\\{\\left(x,\\sin\\frac{1}{x}\\right):x\\in(0,1)\\right\\}\\cup(\\{0\\}\ imes[-1,1])$ 非道路连通。

$\\it Proof$
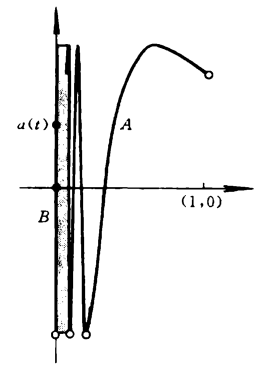
为区别点和区间，用下标 $_p$ 表示点。假设存在道路使得 $a(1)\\in A$ 和 $a(0)=(0,1)_p\\in B$ ，我们来导出矛盾。首先由 $a$ 的连续性可知 $a^{-1}(B)$ 是 $I=[0,1]$ 的闭集。由确界原理，它有上确界 $t_0\\in I$ 并且 $t_0\\in a^{-1}(B)$ ，即 $a(t_0)\\in B$ 。不妨设 $a(t_0)=(0,y_0),y_0\\geq 0$ 。
由 $a$ 连续性，存在 $\\delta>0$ 使得 $\\forall t\\in[t_0,t_0+\\delta]$ 都有 $d(a(t),a(t_0))<1$ 。引入投影映射 $\\pi:X\ o[0,1)$ 将点映成它的横坐标。显然 $\\pi$ 连续，则 $\\pi a$ 也连续，所以 $\\pi a([t_0,t_0+\\delta])$ 是一个区间。它含有 $\\pi a(t_0)=0$ 和 $\\pi a(t_0+\\delta)=x_0>0$ （由 $t_0$ 的定义），所以 $[0,x_0]\\subset\\pi a([t_0,t_0+\\delta])$ 。取充分大的 $n$ 使得 $x_1=1/\\left(2n\\pi-\\frac{\\pi}{2}\\right)\\in(0,x_0)$ ，则存在 $t_1\\in(t_0,t_0+\\delta)$ 使得 $a(t_1)=\\left(x_1,\\sin\\frac{1}{x_1}\\right)_p=(x_1,-1)_p$ ，但是 $d(a(t_1),a(t_0))=d((x_1,-1)_p,(0,y_0)_p)=\\sqrt{x_1^2+(y_0+1)^2}\\geq 1$ ，矛盾！

$\\bf Prop\\ (连续映射保持道路连通)$

设 $f: X\ o Y$ 是连续映射，则 $f$ 把 $X$ 的道路连通子集映成 $Y$ 的道路连通子集。

$\\it Proof$
设 $A\\subset X$ 是道路连通子集，下证 $B=f(A)$ 是 $Y$ 的道路连通子集。设 $y_0,y_1$ 是 $B$ 中两点，取 $x_i\\in f^{-1}(y_i)\\cap A$ 。由 $A$ 的道路连通性可知，存在 $A$ 中道路 $a:I\ o A$ 使得 $a(i)=x_i$ 。注意到 $fa:I\ o A\ o B$ 是 $B$ 中的道路，而且 $fa(i)=y_i$ 。

$\\bf Thm$

若存在 $X$ 的道路连通覆盖（每个成员都是道路连通子集） $\\mathscr{U}$ 和道路连通子集 $A$ 使得 $\\forall U\\in\\mathscr{U},A\\cap U\ eq\\varnothing$ ，则 $X$ 道路连通。

$\\it Proof$
$\\forall x_0,x_1\\in X$ ，则存在 $U_i\\in\\mathscr{U}$ 使得 $x_i\\in U_i$ 。取 $y_i\\in U_i\\cap A$ 。由道路连通性，存在道路 $a:I\ o U_0$ 连接 $x_0,y_0$ 、 $b:I\ o A$ 连接 $y_0,y_1$ 、 $c:I\ o U_1$ 连接 $y_1,x_1$ 。将他们看作 $X$ 中的道路，则它们的乘积 $abc:I\ o X$ 是连接 $x_0,x_1$ 的道路。

由定理可知，两个道路连通子集的有交并是道路连通子集。

$\\bf Prop\\ (道路连通一定连通)$

设 $X$ 是道路连通空间，则 $X$ 也是连通空间。

$\\it Proof$
道路的像集是连通的，因此 $X$ 中任意两点都属于同一个连通子集中。这说明 $X$ 只有一个连通分支。

$\\bf Prop\\ (道路连通性的可乘性)$

道路连通性具有可乘性。

$\\bf Def\\ (道路分支)$

在拓扑空间 $X$ 中定义二元关系： $x\\sim y\\Leftrightarrow x,y$ 可用道路相连，容易证明这是一个等价关系。 $X$ 在等价关系 $\\sim$ 下分成的等价类称为道路连通分支，简称道路分支。显然 $X$ 中的任意道路连通子集都属于唯一的道路分支。

$\\bf Prop$

道路分支是道路连通子集；
对于任意包含道路分支 $A$ 的道路连通子集 $B\\supset A$ ，有 $B=A$ ；
连通分支是一些道路分支的无交并。

$\\it Proof$
有定义可知，对于道路分支 $A$ 中任意两点，都存在 $X$ 中的道路 $a:I\ o X$ 连接它们。由前面的命题可知 $a(I)$ 道路连通，从而它必含于 $A$ 中。也就是说 $a$ 也是 $A$ 中的道路。
取定 $x_0\\in A$ 。则 $\\forall x_1\\in B$ ，存在 $X$ 中的道路连接 $x_0,x_1$ 。这说明 $x_1\\sim x_0$ ，从而 $x_1\\in A$ 。这就证明了 $B\\subset A\\Rightarrow B=A$ 。
因为道路分支都是连通子集，因此必包含于某个连通分支当中。由道路分支和连通分支的唯一性即证。

$\\bf Def\\ (局部（道路）连通)$

如果 $X$ 中每一点的所有（道路）连通邻域构成邻域基，即对于 $\\forall x\\in X$ 的任意邻域 $U$ 都存在 $x$ 的（道路）连通邻域 $V\\subset U$ ，则称 $X$ 是局部（道路）连通空间。

$\\bf Prop\\ (局部（道路）连通的充要条件)$

$X$ 局部（道路）连通 $\\Leftrightarrow X$ 的任意开集作为子空间的（道路）连通分支都是开集（由于开集可以传递开集，这里不必区分是谁的开集）。

$\\it Proof$
$(\\Rightarrow)$ 设 $A\\subset X$ 是开集， $V\\subset A$ 是（道路）连通分支，下证 $V$ 是开集。任取 $x\\in V\\subset A$ ，则 $A$ 是 $x$ 开邻域。由于 $X$ 局部（道路）连通，存在 $x$ 的（道路）连通邻域 $V_0\\subset A$ 。注意到 $x\\in V_0\\cap V$ 非空，所以 $V_0\\cup V$ （道路）连通。由于 $V\\subset V_0\\cup V$ ，由（道路）连通分支的极大性可知 $V=V_0\\cup V$ ，即 $V_0\\subset V$ 。这就说明了 $V$ 中每一点都是内点，从而是开集。
$(\\Leftarrow)$ 任取 $x\\in X$ 和它的任意开邻域 $U$ 。由条件可知 $U$ 作为子空间的包含 $x$ 的（道路）连通分支 $V$ 是开集，从而是 $x$ 的（道路）连通开邻域。