最优化-牛顿法（Newton）_首页-盛煌娱乐-全球商务站

盛煌注册

盛煌动态

最优化-牛顿法（Newton）

发布时间：2024-07-08 21:24:01 点击量：

转：https://blog.csdn.net/qq_36330643/article/details/78003952

平时经常看到牛顿法怎样怎样，一直不得要领，今天下午查了一下维基百科，写写我的认识，很多地方是直观理解，并没有严谨的证明。在我看来，牛顿法至少有两个应用方向，1、求方程的根，2、最优化。牛顿法涉及到方程求导，下面的讨论均是在连续可微的前提下讨论。

1、求解方程。

并不是所有的方程都有求根公式，或者求根公式很复杂，导致求解困难。利用牛顿法，可以迭代求解。

原理是利用泰勒公式，在x0处展开，且展开到一阶，即f(x) = f(x0)+(x－x0)f'(x0)

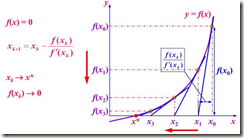
求解方程f(x)=0，即f(x0)+(x-x0)*f'(x0)=0，求解x =?x1=x0－f(x0)/f'(x0)，因为这是利用泰勒公式的一阶展开，f(x) = f(x0)+(x－x0)f'(x0)处并不是完全相等，而是近似相等，这里求得的x1并不能让f（x）=0，只能说f(x1)的值比f(x0)更接近f（x）=0，于是乎，迭代求解的想法就很自然了，可以进而推出x(n+1)=x(n)－f(x(n))/f'(x(n))，通过迭代，这个式子必然在f（x*）=0的时候收敛。整个过程如下图：

2、牛顿法用于最优化

在最优化的问题中，线性最优化至少可以使用单纯行法求解，但对于非线性优化问题，牛顿法提供了一种求解的办法。假设任务是优化一个目标函数f，求函数f的极大极小问题，可以转化为求解函数f的导数f'=0的问题，这样求可以把优化问题看成方程求解问题（f'=0）。剩下的问题就和第一部分提到的牛顿法求解很相似了。

这次为了求解f'=0的根，把f（x）的泰勒展开，展开到2阶形式：

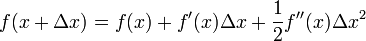
这个式子是成立的，当且仅当?Δx?无线趋近于0。此时上式等价与：

求解：

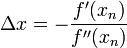
得出迭代公式：

一般认为牛顿法可以利用到曲线本身的信息，比梯度下降法更容易收敛（迭代更少次数），如下图是一个最小化一个目标方程的例子，红色曲线是利用牛顿法迭代求解，绿色曲线是利用梯度下降法求解。

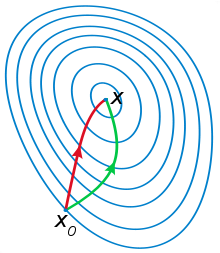
在上面讨论的是2维情况，高维情况的牛顿迭代公式是：

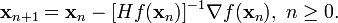
其中H是hessian矩阵，定义为：

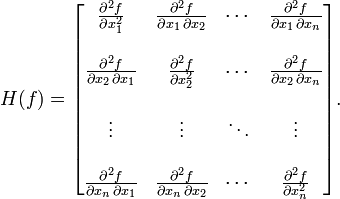
高维情况依然可以用牛顿迭代求解，但是问题是Hessian矩阵引入的复杂性，使得牛顿迭代求解的难度大大增加，但是已经有了解决这个问题的办法就是Quasi-Newton methond，不再直接计算hessian矩阵，而是每一步的时候使用梯度向量更新hessian矩阵的近似。

1、牛顿法应用范围

?牛顿法主要有两个应用方向：1、目标函数最优化求解。例：已知 f(x)的表达形式， $g(x)=\min\left\|{f(x)}\right\|$ ，求? $ming(x)$ ，及g(x)取最小值时的 x ?，即

? 由于||f(x)||通常为误差的二范数，此时这个模型也称为最小二乘模型，即 $\min\{?{f^2}(x)\}$ 。

? 2、方程的求解（根）。例：求方程的解：g(x) = 0，求 x ？

? 这两个应用方面都主要是针对g(x)为非线性函数的情况。2中，如果g(x)为线性情况下的求解通常使用最小二乘法求解。

牛顿法的核心思想是对函数进行泰勒展开。

2、牛顿法用于方程求解

? 对f(x)进行一阶泰勒公式展开：

$g(x){\approx}g({x_k})+g'({x_k})(x-{x_k})$ ? $(1)$

? 此时，将非线性方程 g(x) = 0 近似为线性方程：

$g({x_k})+g'({x_k})(x-{x_k})=0$ ? $(2)$

? 若 f’(x) != 0，则下一次迭代解为：

${x_{k+1}}={x_k}-\frac{1}{?{g'({x_k})}}g({x_k})$ $(3)$

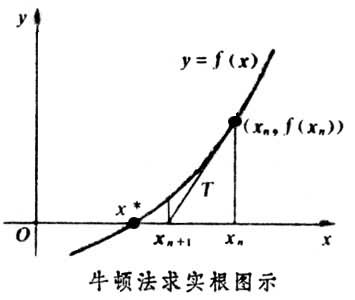
? 牛顿迭代示意图（因此Newton迭代法也称为切线法）：

? 3、牛顿法用于函数最优化求解

对f(x)进行二阶泰勒公式展开：

$g(x){\approx}g({x_k})+g'({x_k})(x-{x_k})+\frac{1}{2}g''({x_k}){(x-{x_k})^2}$ $(4)$

此时，将非线性优化问题 min f(x) 近似为为二次函数的最优化求解问题：

$\min\{g({x_k})+g'({x_k})(x-{x_k})+\frac{1}{2}g''({x_k}){(x-{x_k})^2}\}$ $(5)$

对于（5）式的求解，即二次函数（抛物线函数）求最小值，对（5）式中的函数求导：

$g'({x_k})+g''({x_k})(x-{x_k})=0$ $(6)$

$\Rightarrow{x_{k+1}}={x_k}-\frac{1}{?{g''({x_k})}}g'({x_k})$ ? $(7)$

从本质上来讲，最优化求解问题的迭代形式都是：? ${x_{k+1}}={x_k}-kg'({x_k})$ ，

其中k为系数， $g'({x_k})$ 为函数的梯度（即函数值上升的方向），那么 $-g'({x_k})$ 为下降的方向，

最优化问题的标准形式是：求目标函数最小值，只要每次迭代沿着下降的方向迭代那么将逐渐达到最优，

而牛顿将每次迭代的步长定为： $1/g''({x_k})$ 。

4、补充

a、严格来讲，在“3、牛顿法用于函数最优化求解”中对函数二阶泰勒公式展开求最优值的方法称为：Newton法，

而在“2、牛顿法用于方程求解”中对函数一阶泰勒展开求零点的方法称为：Guass-Newton（高斯牛顿）法。

b、在上面的陈述中，如果x是一个向量，那么公式中：

? $g'({x_k})(x-{x_k})$ 应该写成： $g'{({x_k})^T}(x-{x_k})$ ， $g'({x_k})$ 为Jacobi(雅克比)矩阵。

? $g''({x_k})(x-{x_k})$ 应该写成： ${(x-{x_k})^T}g''({x_k})(x-{x_k})$ ， $g''(x-{x_k})$ 为Hessian（海森）矩阵。

c、牛顿法的优点是收敛速度快，缺点是在用牛顿法进行最优化求解的时候需要求解Hessian矩阵。

因此，如果在目标函数的梯度和Hessian矩阵比较好求的时候应使用Newton法。

牛顿法在进行编程实现的时候有可能会失败，具体原因及解决方法见《最优化方法》-张薇东北大学出版社第155页。

?5、Newton法与Guass-Newton法之间的联系

对于优化问题? $\min\left\|{f(x)}\right\|$ ，即 $\min\{?{f^2}(x)\}$ ，当理论最优值为0时候，这个优化问题就变为了函数求解问题：

$\min\{?{f^2}(x)\}{\Rightarrow}{f^2}(x)=0{\Rightarrow}f(x)=0$

结论：当最优化问题的理论最小值为0时，Newton法求解就可变为Guass-Newton法求解。

另外：对f(x)进行二阶泰勒展开：

? $f(x)=f({x_k})+J{x_k}+0.5{x_k^'}H{x_k}$

f(x)乘以f(x)的转置并忽略二次以上的项：

? ${f^T}(x)f(x)=\{?{f^T}({x_k})+{(J{x_k})^T}+{(0.5{x_k^'}H{x_k})^T}\}$

$*\{f({x_k})+J{x_k}+0.5{x_k^'}H{x_k}\}$

${\rm{=}}{f^T}({x_k})f({x_k})+2f({x_k})J{x_k}+x_k^T{J^T}J{x_k}+f({x_k})x_k^TH{x_k}$

$={f^T}({x_k})f({x_k})+2f({x_k})J{x_k}+x_k^T({J^T}J+f({x_k})H){x_k}$

因此，当 ${x_k}$ 在最优解附近时，即满足 $f({x_k})=0$ ，此时可认为： $H={J^T}J$