大家好!又到了每周一狗熊会的深度学习时间了。在上一期中,小编和大家介绍了机器学习和深度学习中的核心任务以及神经网络的正则化方法和dropout方法来防止过拟合。本期将借着第一期推送小编关于模型与算法的讨论的引子,和大家深入探讨机器学习和深度学习的数学本质,并在此基础上重点介绍深度学习中常用的优化算法。

1
机器学习/深度学习的数学本质
在笔记第一讲的时候,小编就先行讨论了机器学习中的模型和算法的概念的界定。通常而言,我们在听别人口口相传所谓机器学习十大算法之类的概念,久而久之算法成了大家学习机器学习的直接目标。在这样的普遍观点下,线性回归、决策树、神经网络等都被划入算法的范围。对于这种现象,小编有话要说。从根本上来说,如果一定要将线性回归称为算法,也未尝不是什么离经叛道的事情,因为算法本身就是一个广义的概念,包含了如何定义计算规则的意思,但是如果这样的话,那么对平方损失函数进行优化求解的最小二乘由该如何称呼呢?对于线性回归而言,最小二乘法才是算法啊。那线性回归不叫算法又该叫什么呢?叫模型。
在介绍深度学习算法前,小编需要和大家把模型和算法给分一分。在李航老师的统计学习/机器学习方法的概念论述中,一个完整的统计学习方法包括模型、策略和算法三个要素,小编深以为然。模型就是机器学习在所有的模型空间中要采用的模型类别,比如说线性回归和感知机模型,策略则是机器学习方法按照什么的标准去选择最优的模型,通常我们也叫模型评估方法,比如说线性回归的平方损失函数,我们的策略就是要让平方损失函数取到最小值,而算法则是对于策略所选的损失函数采用什么方法取到最小值,即用什么样的计算方法求解最优模型,也就是最优化问题。比如说求解平方损失的最小二乘法以及本文即将介绍的梯度下降法。任何机器学习方法都是由以上三要素构成的。
当我们为一个机器学习方法选择好了模型类别和策略时,机器学习便形式化为一个最优化问题。这些针对损失函数的优化问题,有的是凸函数优化,有的是非凸函数优化。不管怎样,我们需要找到一些高效的算法对损失函数的优化问题进行求解。比如说我们在第二讲中提到的 lasso 的损失函数优化问题就是一个凸函数优化问题。
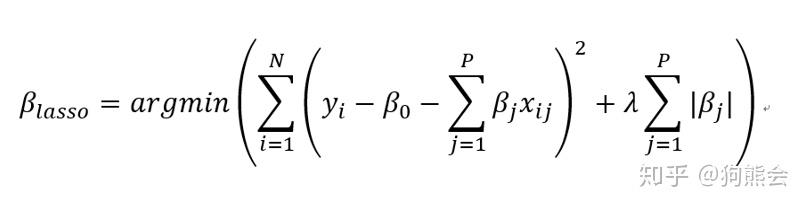
lasso 求解函数
所以,对于大部分的有显式的损失函数表达式而言的机器学习问题,其数学本质都是最优化问题。这也是为什么数学是机器学习和深度学习的基本功的原因所在了。
2
损失函数和深度学习优化算法
对于机器学习中常用的损失函数,比如平方损失、对数损失、合页损失、指数损失和交叉熵损失等等。有不少论文和资料对此做了很多总结,小编不在此细说。具体看参见相关论文。
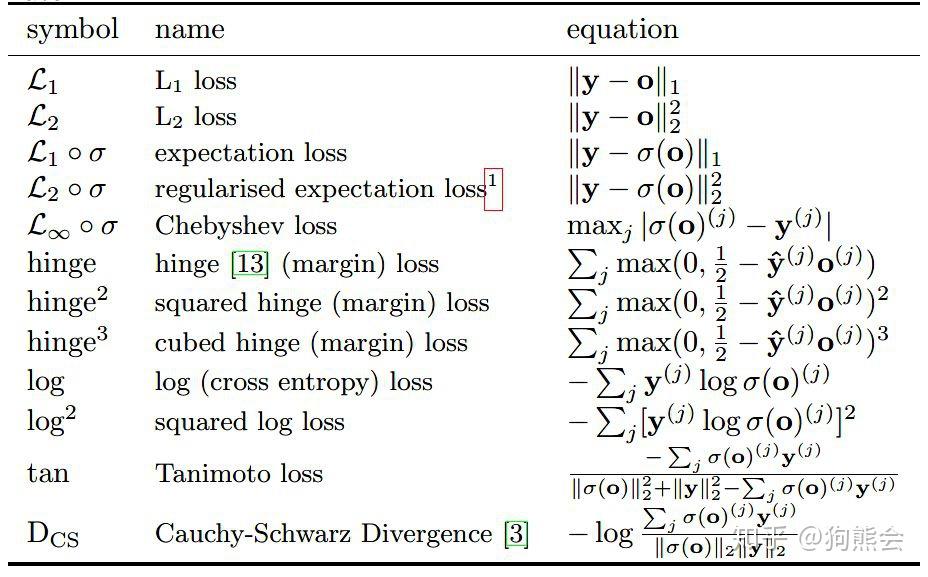
一些损失函数形式
对于神经网络而言,最常用的损失函数要属交叉熵损失函数了。比如说二分类的交叉熵损失长这样:
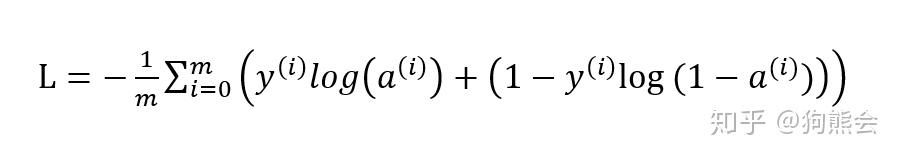
对于交叉熵损失函数的优化,我们通常采用基于梯度下降的算法框架对其进行优化迭代求解。这其中除了原始的梯度下降法之外,根据一次优化所需要的样本量的不同又可分为随机梯度下降和小批量(mini-batch)梯度下降。之后又引入了带有历史梯度加权的带动量(momentum)的梯度下降法、Rmsprop 以及声名远扬的 Adam 算法等等。
下面小编就从梯度下降法开始,对常用的主流深度学习优化算法进行了一个简单的介绍,让大家了解深度学习和神经网络优化求解中常用算法的基本原理,知道神经网络是如何进行优化和参数更新的。以便日后在调包时对于深度学习框架封装好的算法进行使用时,知其然亦知其所以然。
3
梯度下降法
铺垫了两节的内容,终于进入了正题。话不多说,我们先来看梯度下降法(Gradient Descent)。先来给梯度下降法进行一个直观的解释。啥是梯度下降法?基于微积分的观点认为:目标函数关于参数 θ 的梯度方向是函数上升最快的方向。应用到损失函数优化上则是负梯度方向是损失函数下降最快的方向。对于神经网络而言,关于损失函数对权值参数 W 和偏置参数 b 求梯度,并基于负梯度方向进行参数更新:
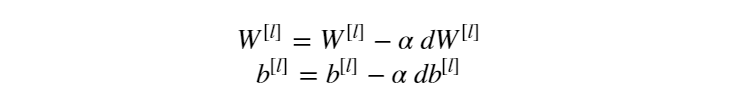
其中 α 为学习率,也叫步长,是个超参数,可以预先指定,也可以通过超参数调优进行选择。以上是梯度下降法的直观解释,那么如何更加通俗的理解梯度下降法呢?且看下图:
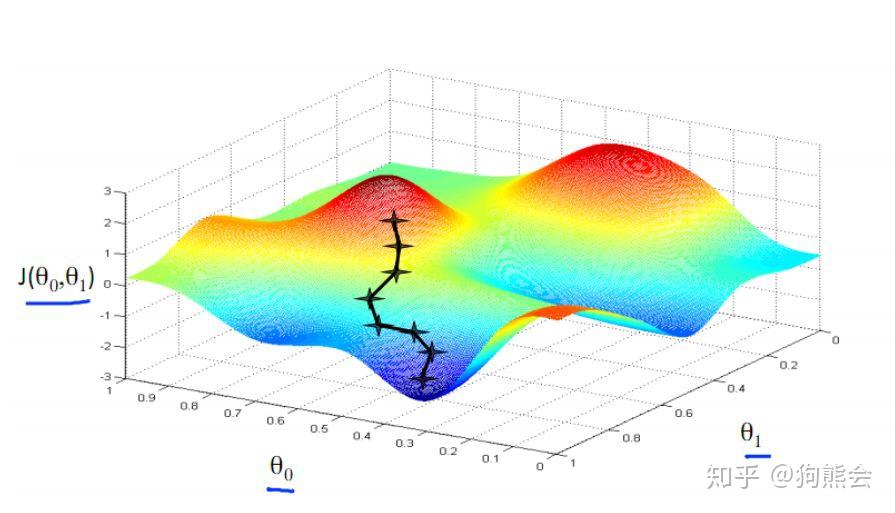
梯度下降法 图片来自吴恩达机器学习课程
假设杨过正站在图中红色区域的山顶,他想要尽快从这陡峭不一的山上下到谷底去找小龙女,那么该如何下山呢?这时杨过举目四望,从四周发现了一个最陡峭的方向,从此下去虽然艰险但速度最快,于是他便下到了一个山腰的一个点,杨过又继续四下查看找最陡峭的方向,继续从这个方向下山,用这个方法一步步不断下降,经过若干次他终于到了谷底与小龙女相会了。是不是很容易理解了?简而言之,梯度下降法就是找最陡峭的方向,也即负梯度方向下降的最多,这便是梯度下降法的一个通俗的比喻。
但在深度学习实际的算法调优中,原始的梯度下降法一般不大好用。通常来说,工业环境下深度学习所处理的数据量都是相当大的。这时若直接使用原始版本的梯度下降,可能训练速度和运算效率会非常低。这时候我们就需要采取一些策略对原始的梯度下降法进行调整来加速训练过程。
这时候将训练数据划分为小批量(mini-batch)进行训练就非常重要了。将训练集划分为一个个子集的小批量数据,相较于原始的整体进行梯度下降的方法,整个神经网络的训练效率会大大提高。这便是小批量(mini-batch)梯度下降。如果批量足够小,小到一批只有一个样本,这时候算法就变成了随机梯度下降(SGD),这时候模型训练起来会很灵活,数据中的噪声也会得到减小。但是随机梯度下降会有一个劣势就是失去了向量化运算带来的训练加速度,算法也较难收敛。因为一次只处理一个样本,虽然足够灵活但效率过于低下。所以在深度学习模型的实际处理中,选择一个不大不小的 batch-size 是一个比较重要的问题。
那么如何选择合适的 batch-size 呢?这个问题可能没有标准答案,一般而言需要视训练的数据量来定,也需要不断的试验。通常而言,batch-size 过小会使得算法偏向 SGD 一点,失去向量化带来的加速效果,算法也不容易收敛,但若是盲目增大 batch-size,一方面会比较吃内存,另一方面是梯度下降的方向很难再有变化,进而影响训练精度。所以一个合适的 batch-size 对于深度学习的训练来说就非常重要,一方面合适的batch-size 会提高内存的利用率,向量化运算带来的并行效率提高,跑完一次 epoch 所需要的迭代次数也会减少,训练速度会加快。这便是小批量(mini-batch)梯度下降 batch-size 的作用。
总而言之,无论是梯度下降法、小批量(mini-batch)梯度下降法还是随机梯度下降法,它们的本质都是基于梯度下降的算法策略,三者的区别即在于执行一次运算所需要的样本量。SGD 与 GD,SGD 与 mini-batch GD 的运算效果如下所示:
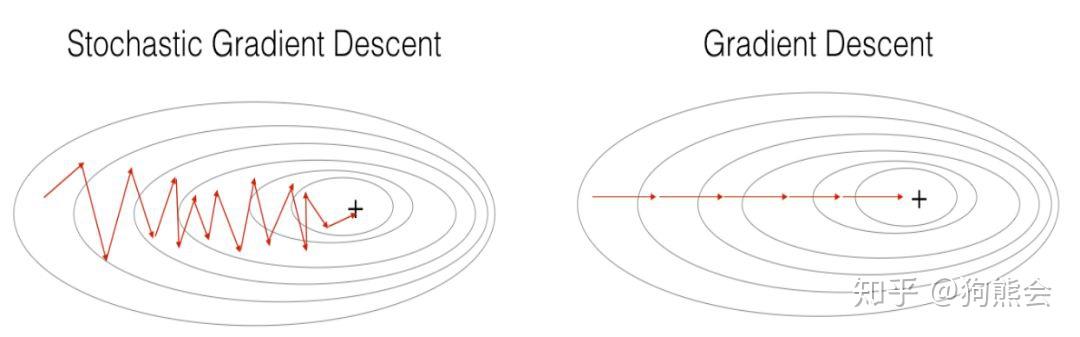
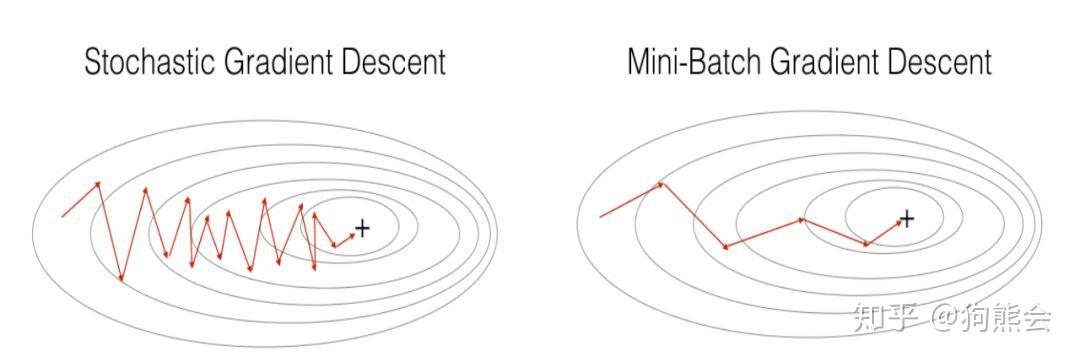
GD vs SGD & Mini-Batch GD vs SGD
图片来自吴恩达deeplearningai课程assignment
4
动量梯度下降:从Momentum到Adam
按说梯度下降法到了 mini-batch 的程度,运算效率也还算可以了。但还是有人觉得慢,在超大的训练数据集面前训练速度仍然不过瘾。如下图的梯度下降所示,从纵轴方向来看,梯度下降算法有一些摆动,我们希望算法在纵轴上能慢一点,因为我们不想要这些摆动,但在横轴上,我们希望加快学习速率,算法能够从左到右快速的收敛到极小值。
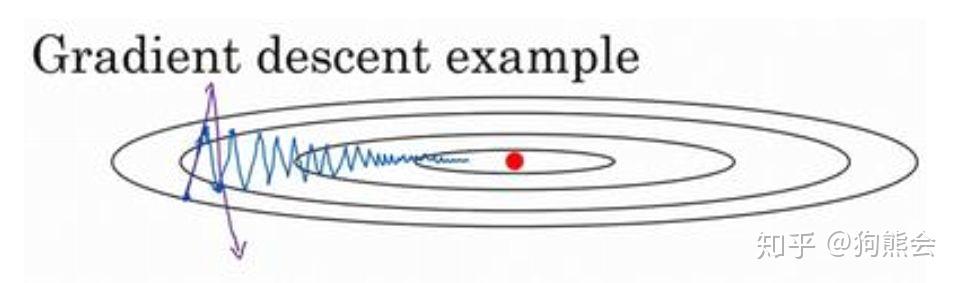
图片来自吴恩达deeplearningai课程
于是有人便基于移动加权的思想,给梯度下降带上了历史梯度的成分来进一步加快速度。这种基于历史梯度和当前梯度进行加权计算的梯度下降法便是动量梯度下降法(Momentum)。
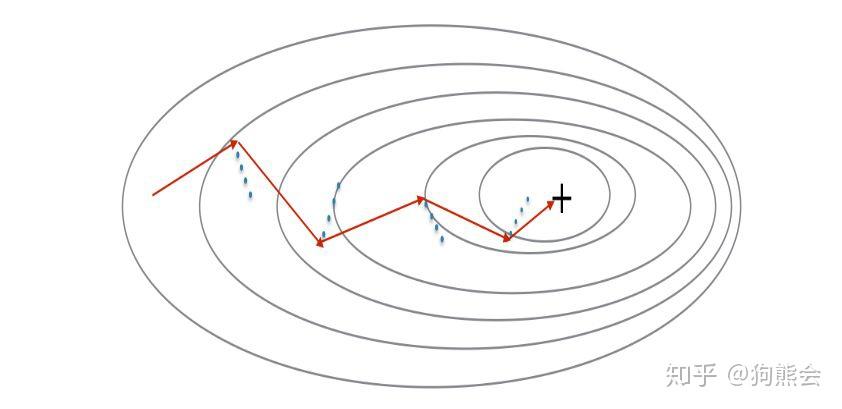
动量梯度下降法的计算公式如下所示:
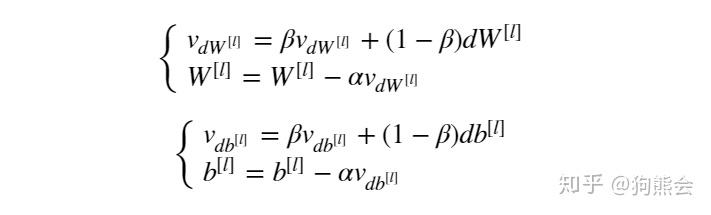
我们以 v 代表为历史梯度,相较于梯度下降法,现在我们有了两个超参数,除了学习率 α 之外,现在又多了个控制梯度加权的参数 β。β 作为超参数通常取值为 0.9,表示平均了过去10次迭代的梯度。大家可以把经过梯度加权后的梯度 v 理解为速率,在进行参数更新时,以速率代替原来的梯度进行更新。以上便是动量梯度下降法(Momentum)的基本原理。
再后来,又有人嫌动量梯度下降法不够快,于是便在动量梯度下降法的基础上去其继续进行了改进,让梯度下降在横轴上更快在纵轴上更慢,于是就有了 RMSprop(均方根加速)(Root Mean Square prop)算法。那么 RMSprop 对于 Momentum 到底做了哪些改进使得训练速度更快呢?相较于 Momentum,RMSprop 最大的变化在于进行历史梯度加权时对当前梯度取了平方,并在参数更新时让当前梯度对历史梯度的开根号后的值做了除法运算。
假设以神经网络的权值 W 的更新方向为横轴方向,偏置 b 的更新方向为纵轴方向,根据前面的表述我们的目的是要加快横轴的速度而减缓纵轴的速度。所以在进行参数更新时,我们会希望 SdW 较小而 Sdb 较大(相较于Momentum,RMSprop用S代替了原先的 v),利用梯度除以二者的均方根正好可以达到这一效果。RMSprop 的计算公式如下:
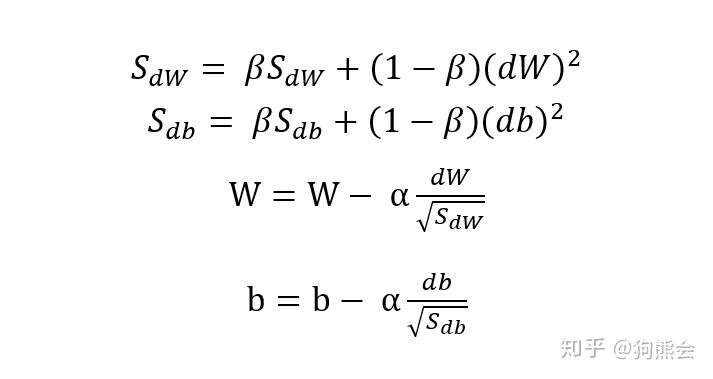
有了以上这么优秀的梯度算法做铺垫,下面小编将继续介绍最后一个深度学习优化算法——Adam。Adam 的全称为 Adaptive Moment Estimation,是一种将之前的动量梯度下降 Momentum 和 RMSprop 结合起来的优化算法,于2014年提出的一种优秀的深度学习优化器:

Adam论文摘要
有了 Momentum 和 RMSprop 的理论基础,小编便不再在 Adam 理论上做过多阐述,我们以权值 W 为例直接看 Adam 的计算公式:
简单描述一下 Adam 算法的计算过程:首先对 Vdw 和 Sdw 进行参数初始化,利用 Momentum 进行梯度加权计算,然后对加权后的梯度进行偏差纠正,这里的参数 t 为迭代次数,β1为 Momentum 的梯度加权超参数。之后利用 RMSprop 算法进行基于梯度平方的更新,然后同样进行偏差纠正。最后将基于 Momentum 和 RMSprop 算法的梯度值进行最终的权值更新。其中 β2 为RMSprop 算法的的梯度加权超参数,ε 为防止分母为零的超参数,通常为一个很小的值。
都说 Adam 算法好,那我们从这些计算公式上又看不出来,小编这里给大家简单说几个:在同等数据量的情况下,Adam 算法占用内存更少,超参数相对固定,几乎不需要怎么调整,很适用于大量训练数据的场景,且对梯度稀疏和梯度噪音有很大的容忍性。
最后以一个动图来展示各种算法的收敛过程:
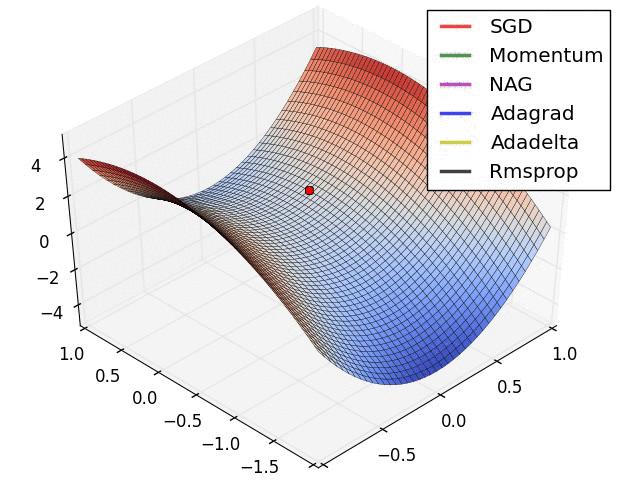
囫囵说了一通,只是大致把几个深度学习的优化算法给大家过了一遍,至于更多的算法理论细节和代码实现,还需要读者各位去找来相应的论文进行认真的研读。还有一些像 NAG 和 Adagrad 等算法并没有全部提及,对深度学习优化算法感兴趣的读者朋友可以找来相关资料进行深入研究。咱们下期见!

【参考资料】
On Loss Functions for Deep Neural Networks in Classification
Kingma D, Ba J. Adam: A Method for Stochastic Optimization[J]. Computer Science, 2014.










